
#TWO TAILED HYPOTHESIS TEST CALCULATOR USING P VALUE HOW TO#
This post will show you both how to calculate, but also how to interpret results which you might see in the papers you read. I get that you now look on the other side of the distribution as well, and therefore I think it's the integral of z(test statistic) + z(-test statistic), but why? I did not get the result -1.645, so I don't understand why I should add the 2.5% of the other side. Hypothesis testing is used in research everywhere, and anyone who has read a white paper has probably seen these kinds of values (p<0.05). But if I do the same procedure with a two-tailed test, SPSS/Excel doubles the p-value.

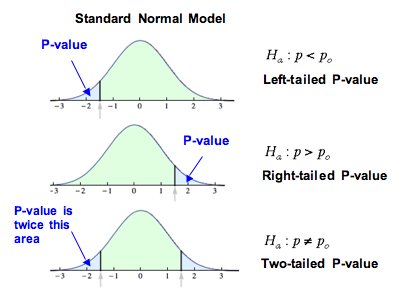
This is easily calculated for a one-tailed test: I just calculate the integral right of the empirical test statisticįor a normal distribution, a z-Value of 1.645 gives me a p-Value of ~0.05. In my understanding, the p-value is the probability to get this or a more extreme test statistics if the H0 is true. I get that in a two-tailed test, you look at both sides of the distribution and therefore you split alpha in half and you need a more extreme test statistic to get a significant result (at the same alpha level). The issue in choosing between one- and two-tailed P values is not whether or not you expect a difference to exist. The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.Since this has been marked as a duplicate, I want to clarify that it's not about critical values of one- vs two-tailed tests, but the calculation of the p-Value in this case. In this example, a two-tailed P value tests the null hypothesis that the drug does not alter the creatinine level a one-tailed P value tests the null hypothesis that the drug does not increase the creatinine level. Instead of using the critical value, we apply the pnorm function to compute the two-tailed p-value of the test statistic. 05 significance level, we do not reject the null hypothesis that the coin toss is fair. These can be solved using the Two Population Calculator. The test statistic 0.89443 lies between the critical values -1.9600 and 1.9600. Sometimes we're interest in hypothesis tests about two population means. Please enter the necessary parameter values, and then click Calculate. The calculator on this page does hypothesis tests for one population mean. This calculator will tell you the one-tailed and two-tailed probability values of a t-test, given the t-value and the degrees of freedom. Confidence intervals can be found using the Confidence Interval Calculator. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. If this is a right tailed test > then the P-Value is 1 minus this number. Hypothesis testing is closely related to the statistical area of confidence intervals. If this is a left tailed test <, then this is the P-Value. For this reason, we call the hypothesis test left, right, or two tailed. For the figure above, with the F test statistic of 1.654, the p-value is 0.4561.
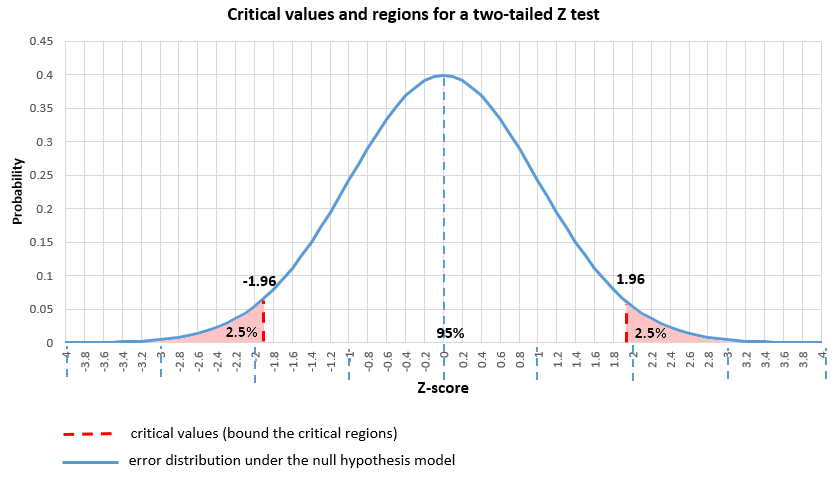
The left tail method, just like the right tail, has a cutoff point. Left tail hypothesis testing is illustrated below: We use left tail hypothesis testing to see if the z score is above the significance level critical value, in which case we cannot reject the hypothesis. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true. When you calculate the p-value and draw the picture, the p-value is the area in. There is left tail, right tail, and two tail hypothesis testing. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. There are two types of errors you can make: Type I Error and Type II Error. When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. If the p-value is inferior or equal to the significance level 0.05, we can reject the null hypothesis and accept the alternative hypothesis. To switch from σ known to σ unknown, click on $\boxed$, reject $H_0$.
Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. If σ is known, our hypothesis test is known as a z test and we use the z distribution. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. The first step in hypothesis testing is to calculate the test statistic.


 0 kommentar(er)
0 kommentar(er)
